0. Primeros pasos
Introducción
En esta sección se detallarán los pasos para empezar a trabajar con el material
del curso usando VS Code y Jupyter notebooks.
Se asume que se han seguido los pasos detallados en
Instalación y
Configuración.
Guía de uso express
VS Code
La pantalla de inicio de VS Code es simple. En el lado izquierdo se encuentra el
ribbon con botones para trabajar. En el centro tenemos accesos directos a
crear o abrir archivos, abrir carpetas o clonar repositorios. También tendremos
la sección Recent donde se verán los archivos o carpetas usados recientemente.
En este curso y en general en nuestro camino en análisis de datos, necesitaremos
organizar nuestro trabajo. Para esto, podemos crear o usar una carpeta dedicada.
Crear o abrir carpeta
Para crear/abrir una carpeta, usamos la opción Open Folder…
VSCode abrirá el Explorador de archivos. Navegamos hasta la carpeta donde
queramos guardar nuestro trabajo. En este caso, cree una carpeta llamada
example_folder en Documentos.
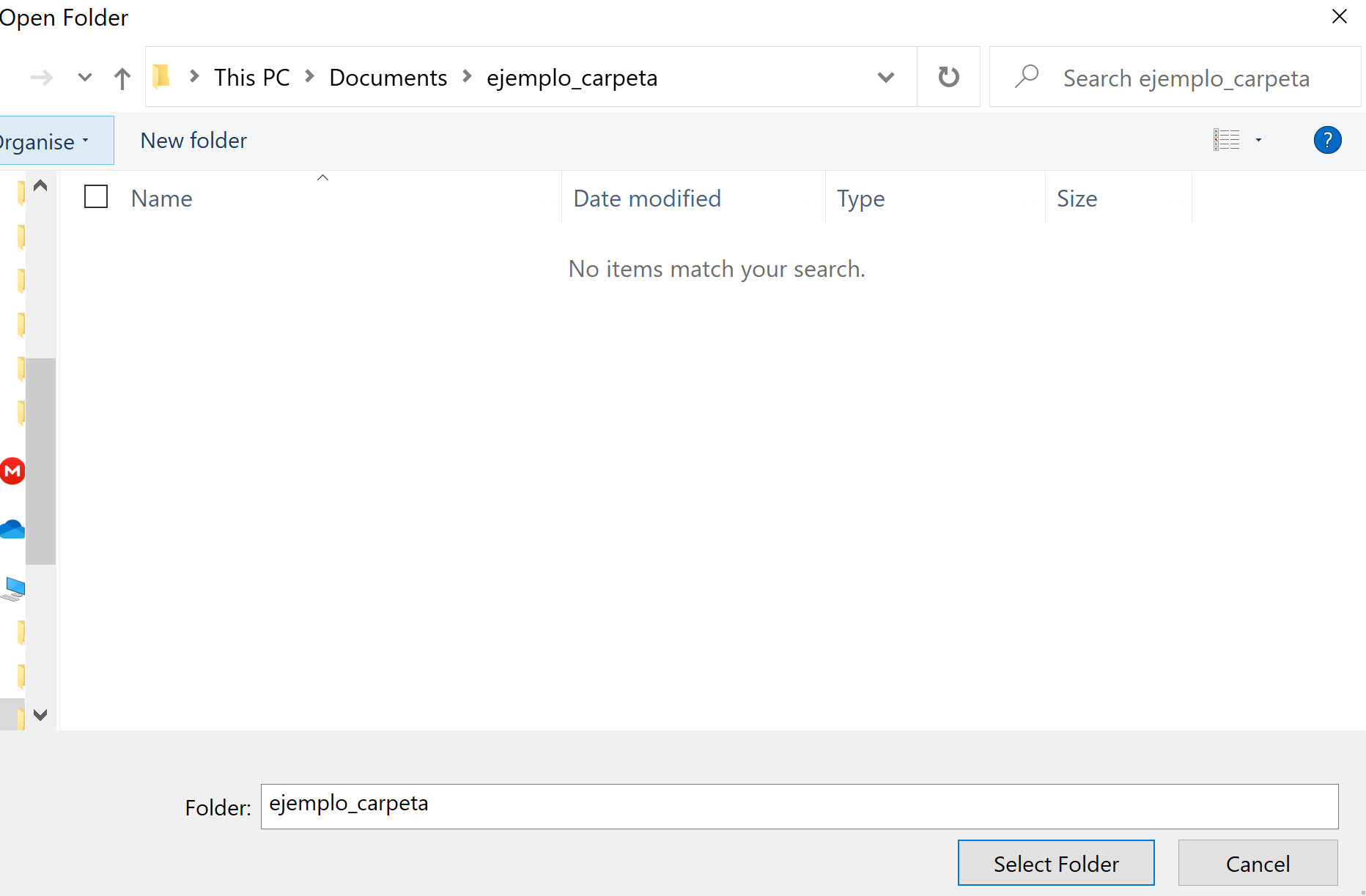
Seleccionamos esta carpeta con el botón Select Folder. Esto nos
regresará a VSCode y veremos algo similar a esto.
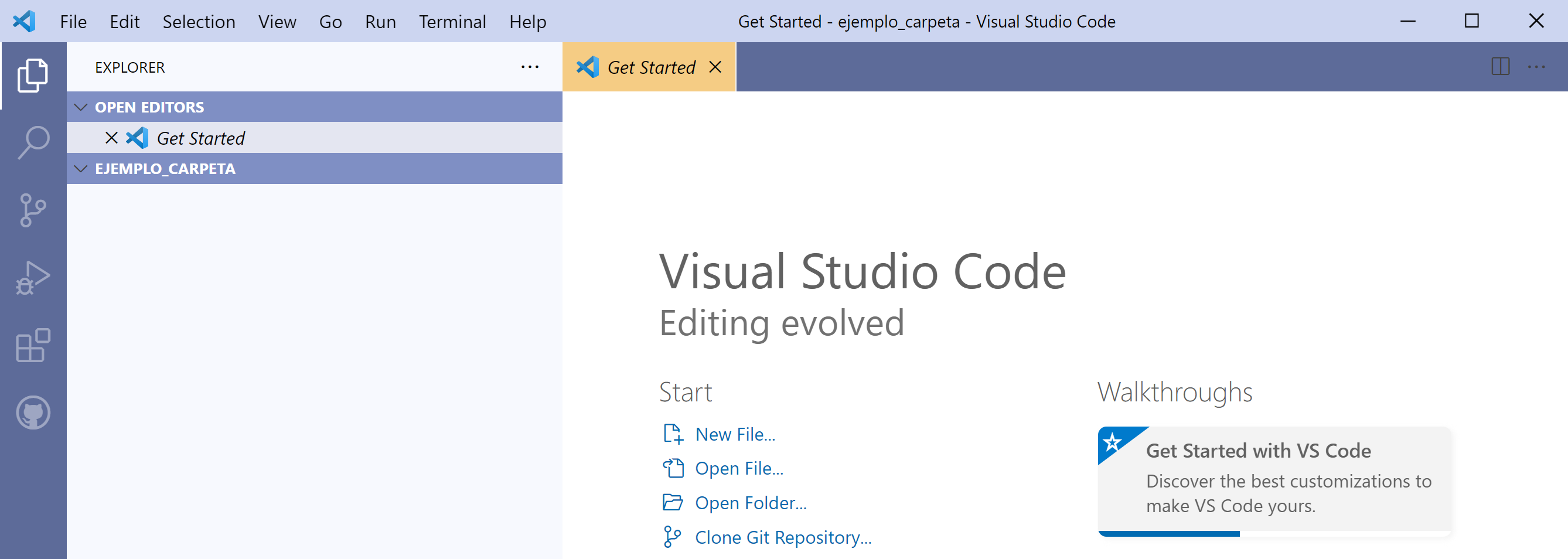
Aquí estamos en la vista Explorer de VSCode, donde podemos explorar lo
que hay en la carpeta que elegimos del lado izquierdo de la ventana. Puesto
que mi carpeta está vacía, (aún) no hay nada que mostrar.
Crear archivos
Una vez que VSCode ha abierto la carpeta donde queremos trabajar,
crearemos un archivo desde VSCode. Para esto, movamos el mouse a la parte
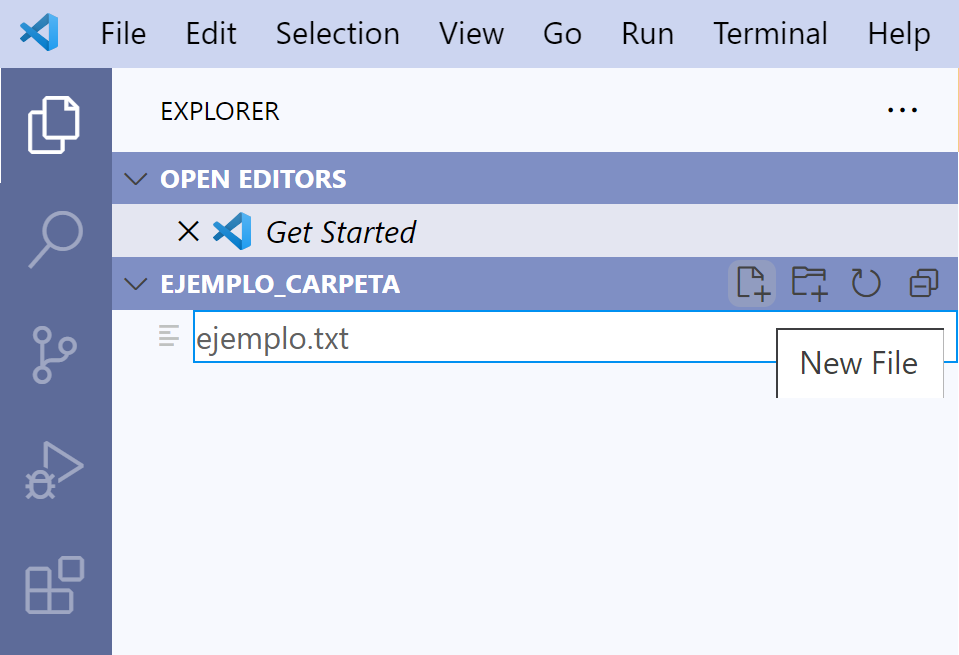
donde se ve el nombre de la carpeta, esto activará cuatro botones. Usaremos
el primer botón New File.
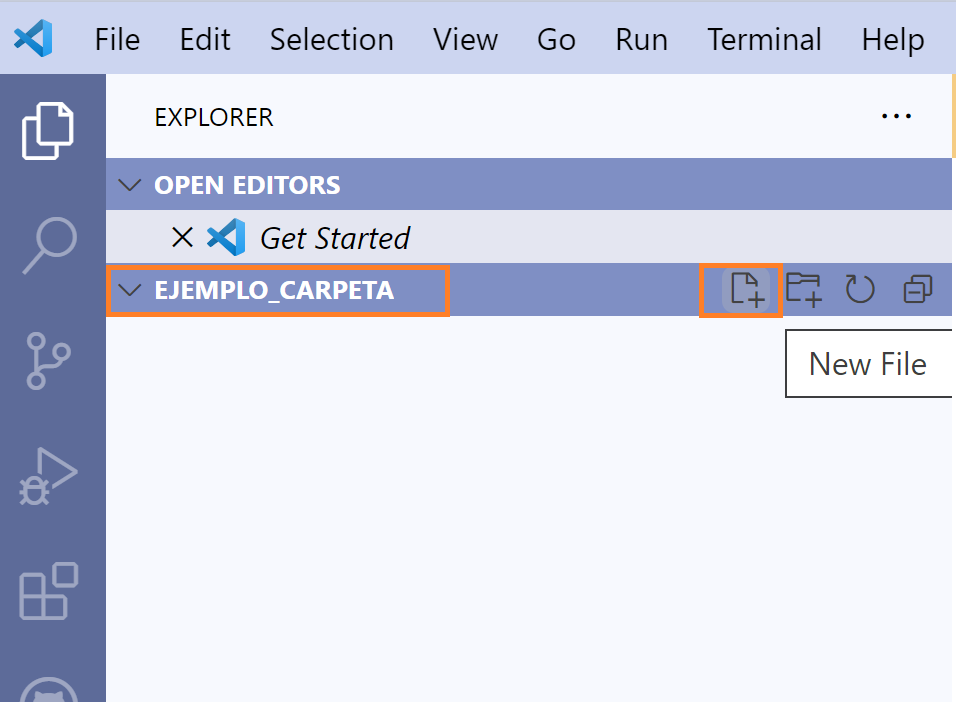
Esto nos permitirá escribir el nombre del archivo. Tip No olvides
escribir la extensión. En este caso, cree un archivo llamado ejemplo.txt.
Presionamos la tecla Enter y listo.
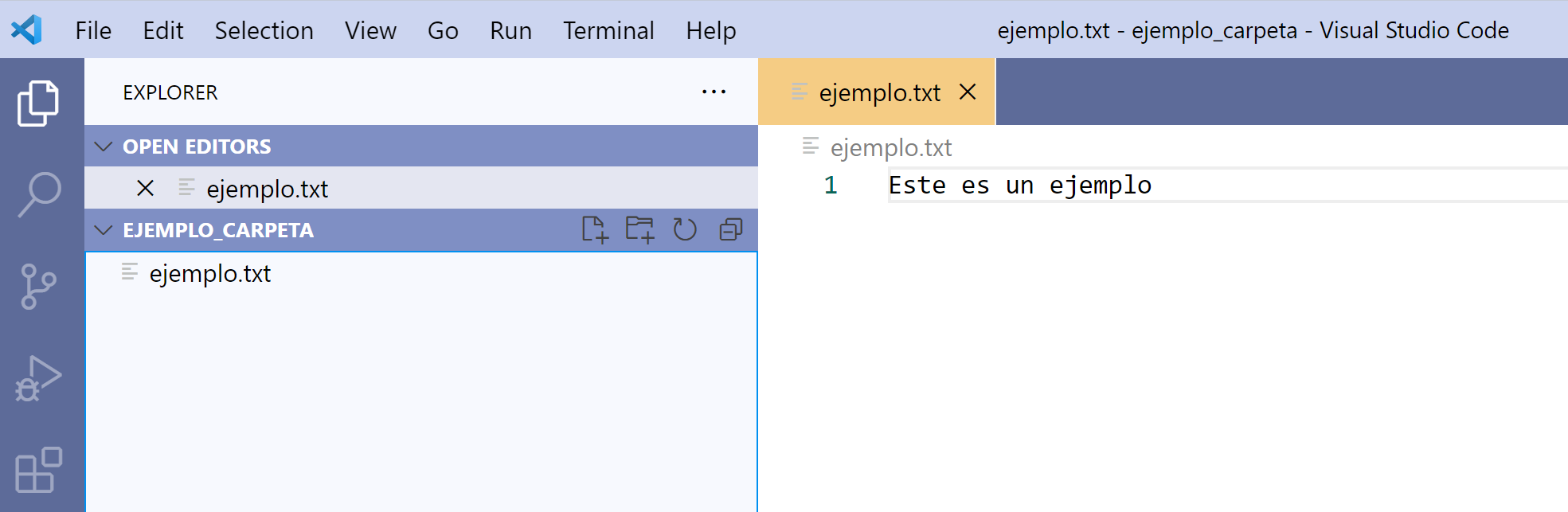
Para editar el archivo, damos click en el nombre del archivo en el
explorador. El archivo se abre como una pestaña en VS Code.
Jupyter notebooks
Jupyter es un entorno donde podemos interactuar con Python de una manera más
sencilla. Con Jupyter podemos ejecutar bloques de código y agregar texto usando
bloques Markdown. La extensión de los archivos es *.ipynb.
Crear Jupyter notebook
Podemos crear un notebook usando el mismo botón New File. En este caso,
cree un archivo llamado ejemplo.ipynb. Presionamos la tecla Enter y listo.
Al abrir el archivo, se mostrará la siguiente interfaz:
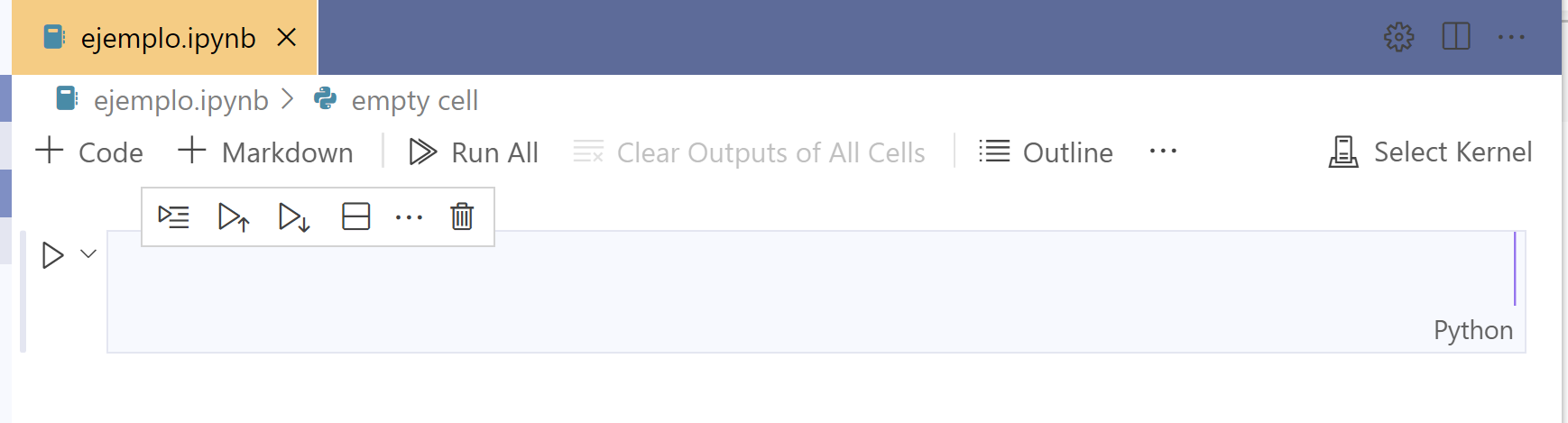
Selección de kernel
Lo primero que tenemos que hacer es seleccionar el Kernel. Kernel es el
intérprete de Python que Jupyter utilizará para ejecutar los bloques de
código. Damos click al botón Select Kernel. Esto nos mostrará la lista
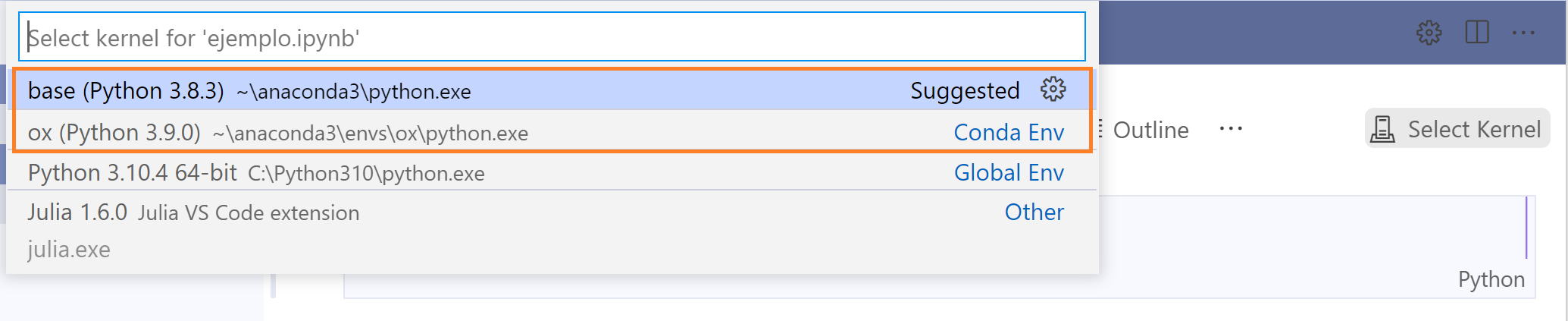
de intérpretes de Python instalados en nuestra máquina.
En mi caso, tengo varios intérpretes, pero elegiré el intérprete base,
que es una distribución de Anaconda.
Consejo
El nombre del intérprete en tu máquina puede ser distinto, asegúrate de
seleccionar el que sea una distribución de Anaconda. La ruta mostrada del
intérprete debe contener la carpeta anaconda3.
Bloque Markdown
Markdown es un lenguaje de marcado simple para dar formato a un texto usando un
editor de texto. Jupyter nos permite agregar bloques Markdown para describir
nuestro trabajo y crear una experiencia similar a trabajar con una libreta de
apuntes.
Creamos una celda Markdown usando el botón + Markdown. Podemos ver que el
bloque Markdown tiene escrito en la esquina inferior derecha la palabra
Markdown.
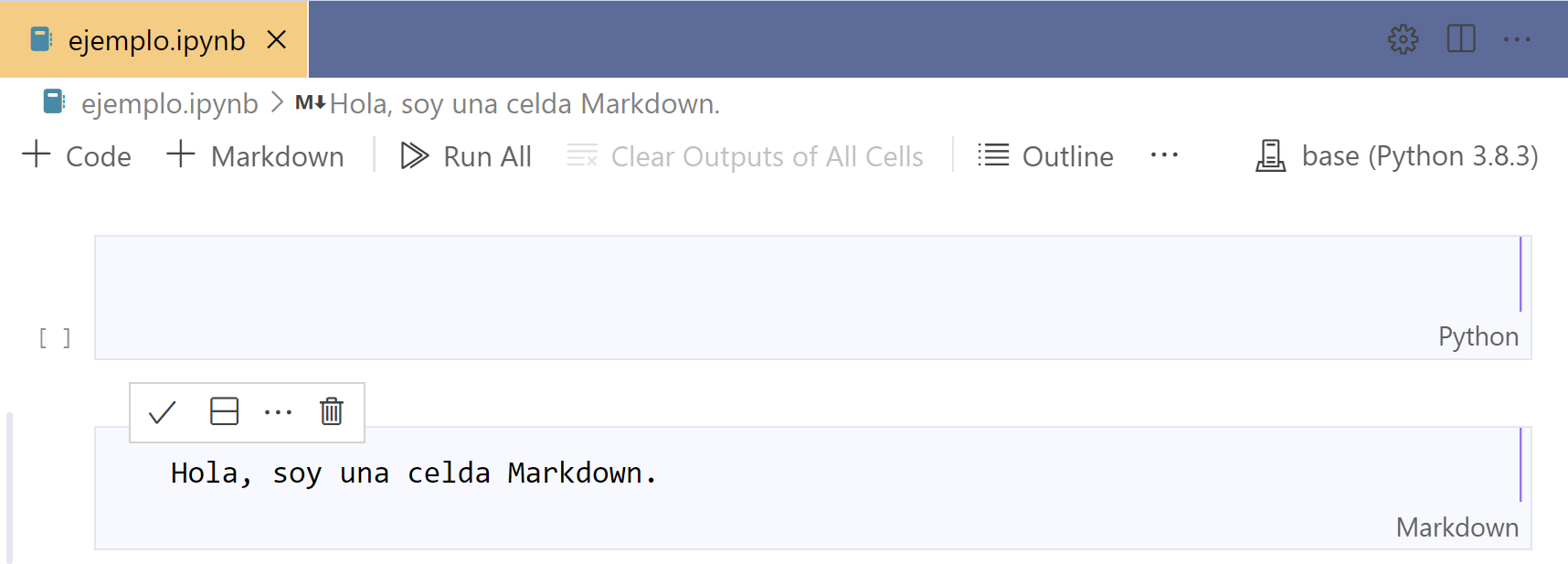
Para guardar lo que acabamos de escribir, damos click en el símbolo
, o usando el atajo Ctrl+Enter
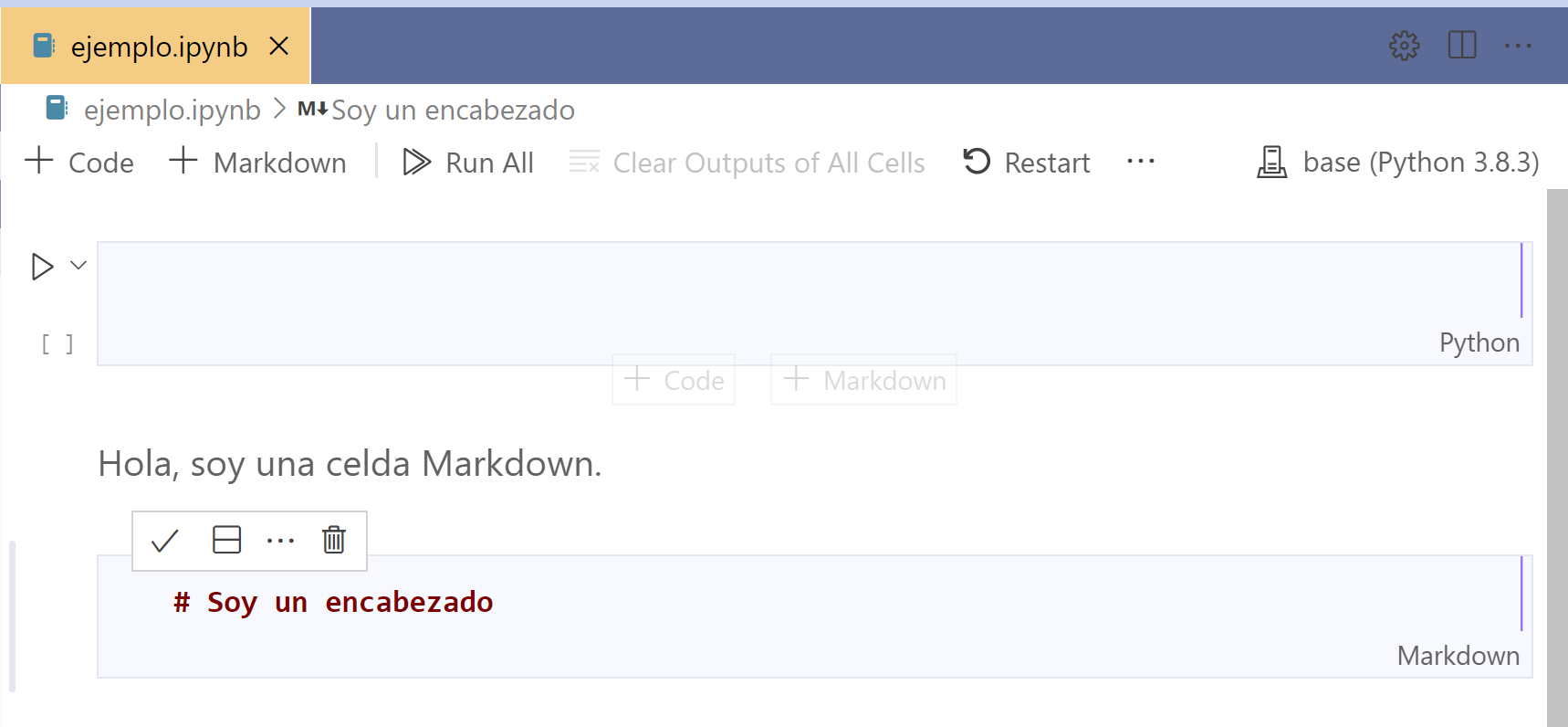
Podemos agregar encabezados anteponiendo el símbolo # al texto.
Más formatos
Copiemos el siguiente ejemplo en un bloque Markdown.
# Encabezado 1
## Encabezado 2
### Encabezado 3
Este es un texto simple.
*Este es un texto en cursiva*
**Este es un texto en negrita**
***Este es un texto en negrita y cursiva***
Este es un ejemplo de los niveles de encabezados que podemos definir con
Markdown. También podemos agregar énfasis al texto usando cursiva y negrita.
The Markdown Guide es una buena
referencia para consultar la sintaxis y buenas prácticas de Markdown.
Bloque de código
Creamos un bloque de código usando el botón + Code. Usaremos este tipo de
bloque para los ejercicios de este curso.
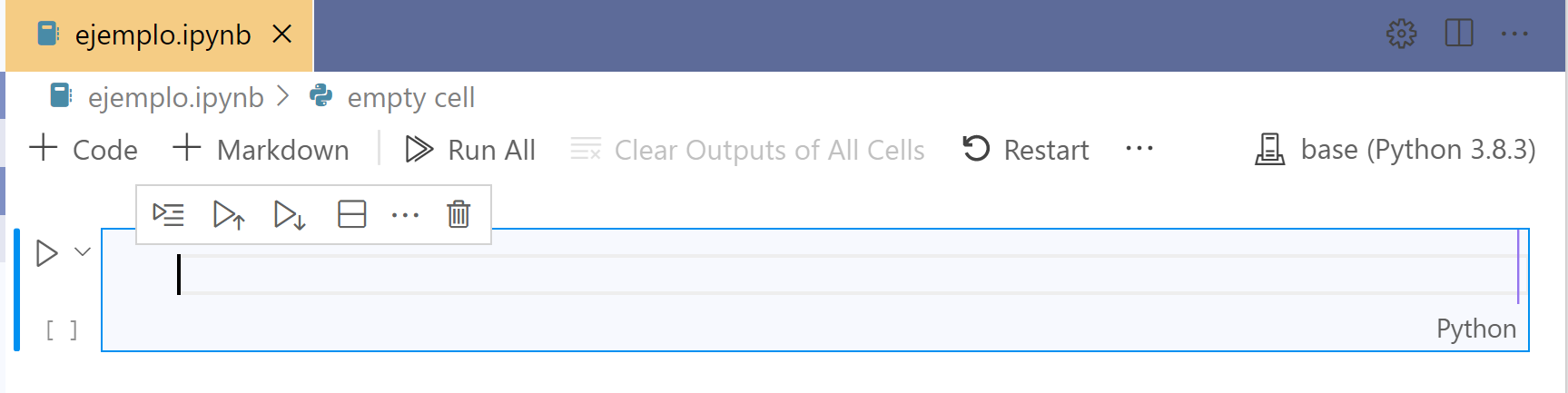
Podemos ver que este tipo de bloque tiene escrito en la esquina inferior
derecha la palabra Python.
Material adicional
1. Introducción a Python
Introducción
Python es un lenguaje de programación fácil de aprender, con estructuras de
datos eficientes. Es considerado como el lenguaje más popular para aprender por
su versatilidad, su enfoque sencillo y la cantidad de librerías disponibles para
machine learning, análisis de datos y visualización de datos.
Salida por pantalla
Lo primero que se suele hacer cuando aprendemos a programar es saludar.
Hello world.
Creemos un Jupyter notebook y agreguemos un bloque de código con las siguientes
líneas de código:
print("Hello world")
print(1+1)
Un comentario
Los comentarios son porciones del código que no se ejecutan. Python utiliza el
símbolo # para definir comentarios.
# Hola, soy un comentario.
print("Hello world")
print(1+1)
# Hola, soy un comentario.
# print("Hello world") # Acabo de comentar esta linea
print(1+1)
Variables
Una variable es una ubicación en memoria que tiene un nombre simbólico asociado
y que puede guardar información.
Declarar una variable es tan fácil como definir un nombre y dar un valor.
Tipo de datos
Python es un lenguaje de tipado dinámico. Es decir, no tenemos que definir el
tipo de dato. Python asumirá el tipo de valor usando una regla llamada
duck typing:
“Si veo un ave que camina como un pato, nada como un pato y suena como un pato,
entonces a esa ave yo la llamo un pato.”
Enteros (int)
a = 1
print(a)
print(type(a))
Flotantes (float)
a = 3.98
print(a)
print(type(a))
a = 1.0
print(a)
print(type(a))
Booleanos (bool)
a = True
print(a)
print(type(a))
a = 1
print(a)
print(type(a))
Cadenas de texto (str)
Convertir tipos de datos
Gracias al duck typing, a veces Python puede asumir un tipo de datos que no
queremos. Sin embargo, podemos convertir datos.
# Esto aunque parezca booleano, Python lo entendera como un entero
bool_test = 1
print(bool_test)
print(type(bool_test))
# Conversion de datos usando bool(), int(), float()
real_bool = bool(1)
real_int = int(2.0)
Entrada por teclado
Podemos permitir que el usuario introduzca información usando la función input().
Esta función nos regresará lo que el usuario escribió como cadena de texto.
# Entrada por teclado usando input()
print("Escriba su nombre")
nombre = input()
# f strings ;)
print(f"Hola, {nombre}")
print(f"La variable tiene el tipo de dato {type(nombre)}")
Estructuras de datos
Una estructura de datos es un formato de organización, manejo y almacenamiento
de datos que permite acceder y modificar datos de forma eficiente.
Python tiene 4 estructuras de datos básicas: listas, sets, tuplas y dictionarios.
En este curso sólo veremos listas y diccionarios.
Listas
Las listas son estructuras de datos que se usan para guardar ítems en una sola
variable. Las listas pueden guardar cualquier tipo de datos.
# Una lista vacia
empty_list = []
str_list = ["1", "2", "3"]
int_list = [1, 2, 3]
mixed_list = [1, 1.0, "2", "Hola", True, "True", [1, 2]]
- Imprimir en pantalla cada una de las listas
- ¿Cuántos elementos tiene la lista?
- Acceder a los elementos de la lista usando índices
# Todo empieza en cero...
print(str_list[0])
print(str_list[3])
- Agregar elementos usando append()
str_list.append("4")
print(str_list[3])
- Eliminar elementos usando remove()
str_list.remove("4")
print(str_list)
print(str_list[3])
Diccionarios
Los diccionarios se usan para guardar datos usando parejas de llaves y valores
(key: value). Los diccionarios no permiten repetición de llaves. Tal y como
funciona un diccionario físico.
# Un diccionario vacio
empty_dict = {}
# Un diccionario de una bolsa de frutas
fruit_bag = {'apples': 4, 'pears': 9, "bananas": 0}
También se puede escribir delimitando espacios (Mira la sangría)
# Un diccionario de una bolsa de frutas, con espacios
fruit_bag = {
'apples': 4,
'pears': 9,
"bananas": 0
}
- Consultar las Keys (Llaves) existentes en el diccionario. Método keys()
- Values (Valores) Método values()
print(fruit_bag.values())
- Comprobar si existe una llave en el diccionario
print("kiwis" in fruit_bag)
- Acceder a valores usando una llave
# Cuantas manzanas hay?
print(fruit_bag["apples"])
# Ahora hay 5 manzanas
fruit_bag["apples"] = 5
print(fruit_bag)
# Agregando kiwis a la bolsa de frutas
fruit_bag["kiwis"] = 1
print(fruit_bag)
- Eliminar una llave usando del
# Ya no es temporada de kiwis
del fruits['kiwis']
print(fruits)
Ejercicios
Crear una variable colegiatura que pida un valor al usuario.
- Imprimir el valor que el usuario introduce
- Imprimir el tipo de dato que tiene
colegiatura - Convertir el valor a float
Usando las listas mixed_list y str_list de los ejercicios:
- Agregar el último elemento de la lista
str_list a la lista
mixed_list - Imprimir en pantalla:
- Tipo de dato del primer elemento de
mixed_list - Elemento con índice 6 de de
mixed_list
- Reto Convertir el elemento con índice 1 de
mixed_list
a tipo int - Reto Verificar si los elementos con índices 0 y 1 de
mixed_list y str_listson del mismo tipo
Seguir el ejercicio de frutas en 5.1. More on Lists en el sitio de
referencia de Python
Estructuras de Datos
Crear un diccionario llamado estudiante con 2 llaves:
Ejercicios:
- Llenar el diccionario con un ejemplo de un estudiante.
- Reto Llenar el diccionario con 3 estudiantes.
Material adicional
2. Primer programa en Python
Introducción
Python es un lenguaje de programación completo que puede realizar distintos tipos
de operaciones: matemáticas, lógicas y relacionales. En esta sección veremos los
operadores que Python utiliza y cómo usarlos.
Operaciones matemáticas
Suma
Se indica con el operador +
Resta
Se indica con el operador -
Multiplicación
Se indica con el operador *
# Multiplicaciones
print(2 * 3)
Potencias
Las potencias se indican con el operador ** (Python no usa ^ para indicar
potencias como otros lenguajes)
# cuidado con el operador...
print(2 ** 3)
Divisiones
Dependiendo lo que se requiera, las divisiones se indican con el operador /,
// o %
# División
print(38 / 5)
# Cociente de la división (devuelve un entero)
print(38 // 5)
# Residuo de la división
print(38 % 5)
Comparadores / Operadores relacionales
Consideremos dos variables, x y y.
# Dos numeros
x = 3
y = 4
Los siguientes operadores devolverán un valor verdadero o falso, dependiendo de
la comparación.
Igualdad
# Igual que
print(x == y)
Desigualdad
# No es igual que
print(x != y)
Menor que, estrictamente menor
Mayor que, estrictamente mayor
Menor o igual que
# Menor o igual que
print(x <= y)
Mayor o igual que
# Mayor o igual que
print(x >= y)
Operadores lógicos
Los operadores lógicos devuelven un resultado si se cumple o no una condición.
Los valores a devolver sólo son dos: verdadero o falso. Estos operadores se
llaman también booleanos por usar álgebra de Boole.
and, operador y
Devuelve un valor verdadero si todas las premisas son verdaderas.
# Y
print(x == y and 5 >= 2)
or, operador o
Devuelve un valor verdadero si al menos una de las premisas es verdadera.
# O
print(x == y or 5 >= 2)
not, operador no
Este operador niega el valor de la premisa. Si el valor de la premisa es
verdadero, el operador devolverá un valor falso. Si el valor de la premisa es
falso, el operador devolverá un valor verdadero.
# not
z = x == y
print(not z)
Estructuras de control
if
if (si, en español) es una sentencia condicional que permite que un programa
ejecute un bloque de código si se cumple una condición (si la condición es
verdadera).
# Sintaxis de if
if condición:
#Aquí va el código que se ejecutará si la condición es verdadera
Sangrías
La sangría es la manera natural de Python de definir bloques de código. Las
sangrías típicamente se definen con un tab.
Fíjate bien en la sangría una vez que definimos la sentencia if. La
sangría define el bloque de código que se ejecutará si dicha condición es
verdadera. Si no dejamos la sangría, dicho bloque de código estará fuera del
if, y seguramente tendremos errores…
El siguiente ejemplo pedirá al usuario que introduzca un número positivo.
Después evaluará si el usuario realmente siguió la instrucción.
numero = int(input("Escribe un número positivo: "))
if numero < 0:
print(f"{numero} no es un número positivo")
print(f"Ha escrito el número {numero}")
El siguiente ejemplo ahora pide al usuario que escriba un número mayor que 5. Si
el usuario escriba un número menor o igual a 5, el programa imprimirá en
pantalla un mensaje informando que esta instrucción no se siguió.
numero = int(input("Escribe un número mayor que 5: "))
if numero <= 5:
print(f"{numero} no es un número estrictamente mayor que 5")
print(f"Ha escrito el número {numero}")
if … else
if … else es una sentencia condicional que permite que un programa ejecute un
bloque de código si se cumple una condición (si la condición es verdadera). Si
la condición no es verdadera, el programa ejecutará el bloque de código contenido
en else.
# Sintaxis de if else
if condición:
# Aquí va el código que se ejecutará si la condición es verdadera
else:
# Aquí va el código que se ejecutará si la condición no es verdadera
El siguiente ejemplo es lo que hace parte del personal de seguridad en la
entrada a un lugar donde es necesario tener mayoría de edad.
print("Entrada del BabyO")
edad = int(input("¿Cuántos años tiene? "))
if edad < 18:
print("No puede entrar")
else:
print("Aunque es mayor de edad, esta lleno...")
if … elif … else
elif (contracción de else if) es una estructura de control útil cuando tenemos
más de una condición a evaluar. De esta manera, podemos encadenar varias
condiciones.
# Sintaxis de if elif else
if condición1:
# Aquí va el código que se ejecutará si la condición1 es verdadera
elif condición2:
# Aquí va el código que se ejecutará si la condición2 es verdadera
else:
# Aquí va el código si ninguna condición es verdadera
El siguiente ejemplo nos dirá cuántos cajeros están disponibles en un banco,
considerando el número de clientes que ya están usando un cajero.
# Multiples condiciones. Un banco con 3 cajeros
cajeros = 3
clientes = int(input("Escriba el numero de clientes usando un cajero "))
# Calcular cajeros disponibles
cajeros_disp = cajeros - clientes
if (cajeros_disp == cajeros):
print("Todos los cajeros estan disponibles!")
elif (1 <= cajeros_disp < cajeros):
print(f"Hay {cajeros_disp} cajeros disponibles")
elif (cajeros_disp == 0):
print(f"No hay cajeros disponibles")
else:
print("Intenta un número mayor que 0 pero menor o igual a 3")
Funciones
Una función es un bloque de código que se ejecuta sólo cuando es llamada o
invocada. Se les puede transferir valores utilizando argumentos y a su vez, una
función puede devolver valores.
Estructura de una función
def mi_funcion(arg):
# Aqui va el codigo
return arg
def otra_funcion(mensaje):
# Aqui va el codigo
print(mensaje)
Las funciones pueden tener más de un argumento. Todo depende de lo que queramos
que el programa realice.
def mi_funcion(arg1, arg2):
# Guarda los argumentos en una lista
arg_list = [arg1, arg2]
return arg_list
Ejercicios
- Escribe una función media que calcule la media de dos números
a y b, y
que imprima el resultado en pantalla.
def media(a, b):
# Aqui va tu codigo
Crea una función temp_convert que tome la temperatura en grados
Farenheit tf como argumento y la convierta a grados Celsius. La función
deberá mostrar en pantalla la temperatura en grados Celsius.
Puedes usar la siguiente ecuación para realizar la conversión de temperaturas:
$$ T_c = \frac{5}{9}(T_f - 32)$$
def temp_convert(tf):
# Aqui va tu codigo
Consejo
Puedes usar la función round(x, 2) para redondear el valor de x a 2
decimales.
Para verificar tu función, puedes usar las siguientes pruebas:
| Prueba | Resultado |
|---|
| temp_convert(59) | 15 |
| temp_convert(32) | 0 |
| temp_convert(-40) | -40 |
- Crea una función llamada contabilidad que tome una lista
pagos con los
pagos del mes y una variable ingresos que indica el total de ingresos del mes
como argumentos. La función deberá regresar el dinero que queda disponible.
def contabilidad(pagos, ingresos):
# Aqui va tu codigo
Consejo
Puedes usar la función sum() para sumar todos los elementos de la lista.
Para verificar tu función, puedes usar las siguientes pruebas:
| Prueba | Resultado |
|---|
| print(contabilidad([100, 300, 20], 750)) | 330 |
| print(contabilidad([300, 39, 700, 500, 220, 740], 2500)) | 1 |
Material adicional
3. Bucles
Introducción
Un bucle es estructura de control que repite un bloque de código con
instrucciones una y otra vez. Los bucles pueden ser finitos (se repiten un
determinado número de veces) o infinitos.
Bucles
For
For es un bucle finito, puesto que definimos el inicio y el fin. Típicamente
se usan cuando conocemos la cantidad de veces que deseamos repetir instrucciones.
Por ejemplo, cuando queremos acceder a una lista por sus elementos.
# Una lista con numeros
a = [1, 2, 10, 0, 6]
for element in a:
print(element)
Range
Range es un tipo de datos especial que representa una secuencia de números. Se
puede utilizar para especificar la cantidad de veces que el bucle For se ejecuta.
range(j) # 0, 1, 2, ..., j-1
range(i, j) # i, i+1, i+2, ..., j-1
range(i, j, k) # i, i+k, i+2k, ..., j-1
Algunos ejemplos:
range_list = list(range(5))
print(range_list)
ten_hundred = list(range(10, 101, 10))
print(ten_hundred)
Usemos ahora range para acceder a los elementos de la lista usando índices.
# Ahora usamos indice
for i in range(len(a)):
print(a[i])
Ejercicio
- Usando un bucle For, calcular la media de un estudiante con las siguientes
calificaciones:
| Materia | Calificaciones |
|---|
| Quimica | 9 |
| Biologia | 8 |
| Matematicas | 9.5 |
| Psicologia | 8.5 |
Consejo
Representa las calificaciones como una lista. Primero sumar y al final, dividir.
$$ \bar{x} = \frac{1}{N}\sum_{i=1}^N x $$
While
While es un bucle de tipo infinito. En él, se repite la ejecución de un bloque de
instrucciones mientras se satisfaga una condición.
El siguiente ejemplo imprimirá en pantalla el número 0 tres veces.
i = 1
while i <= 3:
print(0)
i += 1
print("Hasta que se acabe el dedo")
Otro ejemplo.
i = 10
while i >= 0:
print(i)
i -= 1
print("Cuenta terminada")
Un infinito (Definimos mal la condición a satisfacer)
i = 1
while i <= 10:
print(i)
Casi infinito.
# Are you human?
print("¿Eres una persona? Responde Si o No")
answer = input().lower()
while(answer == "si"):
print("¿En serio? Intenta otra vez. Responde Si o No")
answer = input().lower()
Podemos romper un bucle while con break
def break_loop():
contador = 0
while True:
print("¿Deseas terminar el programa? Escribe Si o No")
respuesta = input()
# Actualizar el contador
contador += 1
if contador >= 5:
print("Ya me ejecuté muchas veces. Voy a descansar.")
break
Ejercicios
Aprobado / No Aprobado
Consideremos el caso de un estudiante que tiene que presentar tres exámenes.
La escala de evaluación es de 0 a 100 puntos.
Un estudiante aprueba el año si:
- Se aprueban todos los exámenes con 40 puntos o más, o
- Se aprueban al menos dos exámenes con 40 puntos o más, y que la media de los
tres exámenes sea estrictamente mayor a 50. (Es decir, una media de 50 puntos no
es aprobatoria).
Escribe una función student_pass que tome tres argumentos, las calificaciones
de los exámenes (como enteros), y determinar si el estudiante ha aprobado el año,
utilizando dichas calificaciones. La función debería imprimir “Aprobado” o
“No aprobado”.
Puedes utilizar la siguientes pruebas para verificar tu función:
| Prueba | Resultado |
|---|
| student_pass(70, 50, 30) | “No aprobado” |
| student_pass(70, 50, 35) | “Aprobado” |
“Dile que no”
Escribe un programa que imprima en pantalla la pregunta
“¿Desea continuar el programa?:”
Y que termine el programa solo cuando el usuario escriba “no”.
def dile_no():
# Aqui va tu codigo
4. Manejo de datos
Introducción
pandas es la librería de Python más utilizada para procesar datos. pandas puede
leer datos de archivos CSV, JSON, txt, xls, xlsx, entre otros. La estructura de
datos más común de esta librería es DataFrame, que es una estructura de datos
tabular bidimensional con ejes etiquetados (filas y columnas).
Datos
Usaremos los siguientes archivos para los ejercicios de este tema:
Primeros pasos
Creamos un Jupyter notebook y creamos un cuadro con código. Analizaremos el
archivo inah_visitantes_2022.csv.
Este archivo contiene la información de visitantes a museos y zonas arqueológicas
manejadas por el INAH durante el año 2022. La descripción de las columnas es la
siguiente:
| Variable | Tipo de variable | Descripción |
|---|
| Estado | Cadena de texto | Estado de la República donde se encuentra el centro INAH |
| Clave_SIINAH | Numérica | Clave interna asociada al centro INAH |
| Tipo | Cadena de texto | Tipo de centro. Z.A. - Zona arqueológica. M. M.H. - Museo o Museo histórico |
| Centro_INAH | Cadena de texto | Nombre del centro INAH |
| Enero_nac | Numérica | Número de visitantes nacionales en el mes de enero |
| Enero_ext | Numérica | Número de visitantes extranjeros en el mes de enero |
| Febrero_nac | Numérica | Número de visitantes nacionales en el mes de febrero |
| Febrero_ext | Numérica | Número de visitantes extranjeros en el mes de febrero |
| Marzo_nac | Numérica | Número de visitantes nacionales en el mes de marzo |
| Marzo_ext | Numérica | Número de visitantes extranjeros en el mes de marzo |
Importar datos
Importamos el CSV usando el método
read_csv().
El nombre del archivo debe ir entre comillas.
import pandas as pd
# Leer el CSV y procesarlo como dataframe
inah_visitantes2022 = pd.read_csv("inah_visitantes_2022.csv")
inah_visitantes2022 es un objeto DataFrame que contiene los datos de este CSV.
Podemos ver lo que contiene el dataframe:
# Miramos lo que contiene el dataframe
inah_visitantes2022
head or tail
Ver sólo ver las primeras n filas con el método
head().
O las últimas n filas con el método tail().
# ver las primeras 5 filas
inah_visitantes2022.head(5)
# ver las últimas 5 filas
inah_visitantes2022.tail(5)
Resumen general
El método info()
muestra información general del DataFrame como el tipo de datos que contiene la
columna, conteo de valores no nulos y uso de memoria.
# Informacion general
inah_visitantes2022.info()
Dimensiones
Para inspeccionar las dimensiones de los datos importados, usamos el atributo
shape.
# Dimensiones
inah_visitantes2022.shape
Esto nos devuelve una tupla (277, 10) que contiene el numero de (filas, columnas)
de este DataFrame.
Columnas
Para inspeccionar el nombre de las columnas, usamos el atributo
columns.
# Columnas
inah_visitantes2022.columns
Ordenar datos
Podemos ordenar datos usando el método
sort_values().
En el siguiente ejemplo, ordenamos por una columna, en orden ascendente.
# Ordenar por una sola columna, "enero_nac". ascending = True por defecto
inah_visitantes2022.sort_values(by=['enero_nac'])
También podemos ordenar por más de una columna, en orden descendente.
# Ordenar por "enero_nac, febrero_nac" en orden descendente
inah_visitantes2022.sort_values(by=['enero_nac', 'febrero_nac'], ascending = False)
DataFrame vs Series
Selección de columnas
Podemos crear un DataFrame más pequeño sólo con algunas columnas.
# Un dataframe con datos nacionales
inah_visitantes_nac = inah_visitantes2022[["Centro INAH", "enero_nac", "febrero_nac", "marzo_nac"]]
# Mostrar 5 primeras filas
inah_visitantes_nac.head(5)
Series
Una serie es un arreglo unidimensional de datos (vector columna).
# Una serie con los datos de los centros INAH
centros_inah = inah_visitantes2022["Centro INAH"]
centros_inah
# Series pueden ser convertidas a lista
enero_nac = inah_visitantes2022["enero_nac"].to_list()
Estadística descriptiva
DataFrame
Accedemos a las siguientes medidas descriptivas de los datos usando el método
describe():
- Conteo
- Media
- Desviación típica
- Valor mínimo
- Primer cuartil (25%)
- Segundo cuartil o mediana (50%)
- Tercer cuartil (75%)
- Valor máximo
# Mostrar estadistica descriptiva de un DataFrame
inah_visitantes2022.describe()
Series
Para una serie con valores numéricos, se reportan las mismas medidas que en un
DataFrame. Pero para una serie con valores de texto, se reportan:
- Conteo
- Valores únicos
- Top (Valor más frecuente)
- Frecuencia
# Mostrar estadistica descriptiva de una Serie
inah_visitantes2022["Estado"].describe()
Operaciones
Hemos visto hasta ahora como importar datos y ver sus medidas de estadística
descriptiva, pero también podemos realizar operaciones con los DataFrames.
Crear columnas
Crear columnas es tan simple como declarar el nombre de la columna y los valores
que queremos guardar en esta columna.
Por ejemplo, creemos la columna “prueba_columna” en el DataFrame de visitantes
a centros INAH. Le asignaremos a esta columna un valor arbitrario.
inah_visitantes2022["prueba_columna"] = 1
Lo que hizo este instrucción fue crear la columna y asignar a todas las filas el
valor de 1. Pero, también podemos crear columnas usando valores de otras columnas
usando operaciones matemáticas.
Creemos una nueva columna llamada enero_visitantes que contenga la suma de
todos los visitantes (tanto nacionales como extranjeros) de cada centro INAH en
el mes de enero.
# enero_visitantes es la suma de visitantes nacionales y visitantes extranjeros
inah_visitantes2022["enero_visitantes"] = inah_visitantes2022["enero_nac"] + inah_visitantes2022["enero_ext"]
Eliminar columnas
Para eliminar columnas innecesarias o que fueron creadas por error, se puede
hacer con el método
drop().
La sintaxis es la siguiente:
donde el argumento columns puede aceptar un valor único con el nombre de la
columna, o una lista con los nombres de columnas a eliminar.
Para eliminar la columna que acabamos de crear, introducimos la siguiente
instrucción:
inah_visitantes2022 = inah_visitantes2022.drop(columns = "prueba_columna")
Crear columnas usando funciones
Para usar una función basada en una columna podemos usar el método
map().
La sintaxis es la siguiente:
# Sintaxis de map
df['nueva_col'] = df['col'].map(funcion)
Tenemos la siguiente función que escribe una cadena de texto si la columna tiene
valores de 0 o distintos de 0.
def test_function(col):
if col == 0:
col = "No visitantes"
else:
col = "Visitantes"
return col
Usemos map para aplicar esta función a una nueva columna “respuesta”.
inah_visitantes2022["respuesta"] = inah_visitantes2022["enero_nac"].map(test_function)
inah_visitantes2022.head()
Información
Si la función es más compleja y requiere más de una columna, está el método
apply().
Selección de datos
Podemos hacer una selección de datos del DataFrame, dependiendo si queremos ver
un subconjunto que satisfaga una o más condiciones, o la ubicación dentro del
DataFrame.
Condicionales
- Una condición
# Sintaxis
df[df["columna"] condición]
donde la condición puede ser una igualdad ==, diferente de !=, mayor o igual
>=, menor o igual <=, estrictamente mayor > o estrictamente menor <.
# Mostrar datos solo para el estado Guerrero
inah_visitantes2022[inah_visitantes2022["Estado"] == "Guerrero"]
# Mostrar centros con más de 1000 visitantes nacionales en enero
inah_visitantes2022[inah_visitantes2022["enero_nac"] >= 10000]
- Múltiples condiciones
# Sintaxis
df[(df["columna"] condición1) operador_lógico (df["columna"] condición2) ... ]
donde el operador lógico puede ser & (operador “y”) o | (operador “o”)
# Mostrar los centros con más de 1000 visitantes nacionales en Guerrero
inah_visitantes2022[(inah_visitantes2022["Estado"] == "Guerrero") & (inah_visitantes2022["enero_nac"] > 1000)]
- Múltiples valores a comparar de una misma columna
El método isin()
nos permite utilizar una lista para comparar valores.
# Sintaxis
df[df["columna"].isin(lista)]
Mostrar los centros con más de 1000 visitantes nacionales en Guerrero y Quintana
Roo en el mes de marzo.
# Seleccion de centros en Guerrero y Quintana Roo usando el metodo isin
inah_visitantes2022[(inah_visitantes2022["Estado"].isin(["Guerrero", "Quintana Roo"])) & (inah_visitantes2022["marzo_nac"] > 1000)]
- Query
Cuando se tiene más de una condición,
query()
puede ser más elegante.
# Sintaxis
df.query('expresion')
Para seleccionar los datos de centros INAH del estado de Guerrero con visitantes
nacionales en enero mayores o igual a 1000, podriamos escribirlo como en el
ejemplo 2, o usando query:
# Seleccion usando query
inah_visitantes2022.query('Estado == "Guerrero" & enero_nac >= 1000')
Ver valores por su label, o utilizando con condiciones, .loc
loc es
una propiedad que nos permite ver valores usando el label (o índice) de las filas,
o usar condiciones para generar vistas.
# Vistas por condiciones. Tambien se pueden definir cuantas columnas mostrar
inah_visitantes2022.loc[inah_visitantes2022["Estado"] == "Guerrero", ["enero_nac", "febrero_nac"]]
Parece igual…
# Un DataFrame con labels en lugar de indices
df_label = pd.DataFrame([[1, 2], [4, 5], [7, 8]],
index=['cobra', 'viper', 'sidewinder'],
columns=['max_speed', 'shield'])
# loc, vistas por label
df_label.loc["cobra"]
Ver valores por índices, .iloc
iloc
es una propiedad que nos permitirá acceder a filas y columnas usando sus índices.
# Sintaxis general
df.iloc[fila_a: fila_b, columna_a: columna_b]
- Una fila
# Primera fila, una serie
inah_visitantes2022.iloc[0]
# Primera fila, pero un dataframe
inah_visitantes2022.iloc[[0]]
- Más de una fila, en desorden
# Más de una fila, en distinto orden
inah_visitantes2022.iloc[[7, 2, 0]]
- Celdas
# Celda ubicada en la fila 0, columna 3
inah_visitantes2022.iloc[0,3]
- Mostrar una selección de filas, en orden.
# Mostrar las filas 0, 1 y 2
inah_visitantes2022.iloc[0:3]
- Mostrar selección de filas y de columnas
# Mostrar las primeras (0:2) filas, las primeras 3 columnas (0:3)
inah_visitantes2022.iloc[0:2,0:3]
Agrupación de datos
groupby()
es un método que permite agrupar datos por columnas y crear un DataFrame más
compacto.
La sintaxis de este método es:
# Sintaxis
df.groupby(by = "nombre_columna").funcion()
Se requiere que definamos una función para que pandas pueda aplicar una
operación matemática para presentar los valores agrupados. La función puede ser:
- count() – Conteo
- sum() – Suma
- mean() – Media
- median() – Mediana
- min() – Valor mínimo
- max() – Valor máximo
- std() – Desviación tipica
- var() – Varianza
Agrupemos los datos de visitantes a centros INAH usando la columna estado,
sumando los valores.
# Agrupar datos por estado, sumando valores
inah_visitantes2022.groupby(by = "Estado").sum()
Remodelación usando “Melt”
A veces necesitaremos de “masajear” un DataFrame para convertir de un formato
ancho a un formato largo. Esto se logra con el método
melt().
Este tipo de remodelación de DataFrames es de utilidad cuando se tienen una o
más columnas que pueden ser usadas como identificadores, y las demás columnas
como valores.
# Remodelando el df
pd.melt(inah_visitantes2022)
Ejercicios
Usando los datos en estudiantes_mxuk.csv, contestar las siguientes
preguntas.
- ¿Cuántos estudiantes de Puebla estudian un posgrado?
- ¿Cuál es la edad promedio de los estudiantes que estudian un posgrado?
- Seleccionar los registros que satisfagan las siguientes condiciones:
- Estudiantes mayores de 27 años y que no son de CDMX.
- Estudiantes menores de 28 años y, que estudian en University of York y en
University of Sussex.
- Calcular (tal vez sea útil usar
groupby()):- Número de estudiantes por universidad
- Número de estudiantes por estado
- ¿Cuál es la universidad con más estudiantes mexicanos?
Referencias
5. Visualización
Introducción
La información que hemos procesado previamente se puede visualizar usando
gráficos. En esta sección veremos como crear gráficos profesionales con
matplotlib y seaborn.
Datos
Usaremos los siguientes archivos para los ejercicios de este tema:
Librerías
Usaremos las siguientes librerías para los ejercicios de este tema:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams["figure.figsize"] = (10,8) # Definicion de tamaño en pulgadas
Descripción de datos
Estos son datos abiertos de aspirantes a posgrados ofrecidos en el Instituto de
Ecología, A.C. (INECOL). La descripción de las columnas es la siguiente:
| Variable | Tipo de variable | Descripción |
|---|
| id_aspirante | Numérica | Número de identificación interno asignado al aspirante |
| calificacion_ingles | Numérica | Calificación obtenida en prueba de inglés. Escala 0 - 10 |
| calificacion_conocimientos_tecnicos | Numérica | Calificación obtenida en prueba conocimientos técnicos. Escala 0 - 10 |
| entrevista | Numérica | Calificación obtenida en entrevista. Escala 0 - 10 |
| desempeno_academico | Numérica | Calificación obtenida por desempeño académico. Escala 0 - 10 |
| calificacion_final | Numérica | Calificación final asignada al aspirante. Escala 0 - 10 |
| resultado | Texto (Categórica) | Resultado del proceso de admisión |
matplotlib
matplotlib es una librería de bajo nivel, es decir, necesitamos definir muchas
cosas, pero tendremos más libertad y flexibilidad en nuestros gráficos.
Revisaremos las gráficas de dispersión en este paquete.
Dispersión
Vamos a utilizar datos artificiales de una variable x, y creamos dos funciones
de x.
import numpy as np # Libreria para acceder a funciones matematicas
x = np.linspace(-3, 3, 100) # crear 100 valores en un rango -3 a 3
y1 = 3*x
y2 = x**3 + x**2 - x + 1
# Crear un grafico con ambas curvas en el mismo eje
fig, ax = plt.subplots()
ax.plot(x, y1, 'g--', label=r'$y_1$') # Trazos
ax.plot(x, y2, 'y.', label=r'$y_2$') # Puntos
# .legend() utiliza el argumento "label" para cada curva
ax.legend(loc='lower right', fontsize=14)
# Mostrar el grafico
plt.show()
seaborn
seaborn es una librería basada en matplotlib, pero es de alto nivel. Es decir,
no tendremos que escribir tanto para crear gráficos.
Ahora usaremos los datos de aspirantes a posgrado de INECOL, que están en el
archivo aspirantes_inecol2020.csv.
# Importar datos aspirantes INECOL
inecol_df = pd.read_csv("aspirantes_inecol2020.csv")
Diagrama de pares (pair plot)
Este diagrama nos puede servir para encontrar relaciones entre variables y como
primer paso en nuestro análisis de datos. El diagrama de pares genera una matriz
con gráficos de dispersión que relaciona parejas de variables en el conjunto
de datos. En la diagonal se muestra la distribución de la variable usando un
histograma.
# Dale unos segundos...
sns.pairplot(data = inecol_df)
seaborn nos permite generar un diagrama de pares distinguiendo valores en las
gráficas de dispersión e histogramas en función de una variable categórica con
el argumento hue. En los datos de INECOL, la variable resultado es una
variable categórica pues define si el estudiante fue aceptado con beca, aceptado
sin beca o no aceptado.
# agregando hue
sns.pairplot(data = inecol_df, hue = "resultado")
Gráfico de dispersión
En lugar de escribir un montón de código, seaborn tiene un método que simplifica
esta tarea. Al ser un gráfico de dispersión, no une los puntos.
# Dispersion
sns.scatterplot(data = inecol_df, x = "calificacion_ingles", y = "calificacion_final")
Gráfico de línea
Este gráfico es similar al de dispersión, pero en este gráfico, seaborn une los
puntos. Debido a que las medidas pueden ser ruidosas, seaborn estima la
tendencia central de los datos y es lo que nos muestra trazado en una línea.
Además, muestra el intervalo de confianza ci de 95% de dicha tendencia.
Hagamos un gráfico de línea de la calificación final del aspirante
calificacion_final respecto a la calificación obtenida en la prueba de inglés
calificacion_ingles.
# Lineplot de calificacion_final respecto a calificacion_ingles
sns.lineplot(data = inecol_df, x = "calificacion_ingles", y = "calificacion_final")
Esta gráfica puede graficar la desviación típica en lugar del intervalo de
confianza usando el argumento ci = "sd", o no mostrar nada con ci = None.
Histograma
Un histograma es una visualización que muestra gráficamente la distribución de
variables numéricas utilizando barras.
La sintaxis básica de seaborn para generar histogramas es la siguiente:
# Sintaxis
sns.histplot(data = df, x = "columna", stat, kde)
donde
stat es un parámetro opcional para definir la medida estadística utilizada
para determinar la frecuencia de los valores de la variable. seaborn puede
utilizar las siguientes medidas:
count: número de observaciones en cada segmento. Este es el comportamiento
predeterminadofrequency: muestra el número de observaciones dividido entre el “ancho”
(intervalo) del segmentoprobability: normaliza el eje para que la altura de las barras sumen 1percent: normaliza el eje para que la altura de las barras sumen 100density: normaliza el eje para que el total del área del histograma sea 1
kde es un parámetro opcional donde podemos obtener una distribución estimada
de los datos. Para activarlo pasamos el siguiente argumento cuando creemos el
objeto histoplot: kde = True
Generemos el histograma de la calificación final utilizando porcentaje como
medida estadística.
sns.histplot(data = inecol_df, x = "calificacion_final", stat = "percent")
Diagramas de caja y bigotes (box plot)
Este diagrama muestra la distribución de datos cuantitativos utilizando sus
medidas de localización.
# Ver la distribución de calificaciones finales de los aspirantes con boxplot
# (Se ve mejor así, que si invirtieramos los ejes...)
sns.boxplot(data = inecol_df, y = "resultado", x = "calificacion_final", whis = 1.5)
whis es un parámetro opcional que define la extensión de los “bigotes” de las
cajas, respecto al rango intercuartílico. En el ejemplo de arriba, 1.5 es 1.5
veces el rango intercuartílico.
Diagrama de violín
Visualización combinada de un diagrama de cajas y de la distribución estimada de
los datos.
# Ver la distribución de calificaciones finales de los aspirantes con violinplot
sns.violinplot(data = inecol_df, y = "resultado", x = "calificacion_final")
Gráfico de barras
Podemos agrupar los datos usando la columna “resultado”, contando el número de
registros.
# Agrupar por Resultado y recrear el indice
inecol_resultado = inecol_df.groupby(by = "resultado").count()
# Recrear el indice para que "resultado" no sea indice
inecol_resultado = inecol_resultado.reset_index()
¿Por qué reset_index()?
Al agrupar los valores con groupby(), la columna usada como argumento de by se
convierte en el índice del DataFrame compacto.
Si deseamos que el índice sea numérico y no la columna, la función
reset_index()
nos sirve para recrear el índice numérico.
# Gráfico de barras resumiendo el resultado final de aspirantes
sns.barplot(data = inecol_resultado, y = "resultado", x = "calificacion_final")
Usando los datos del INAH, creemos un gráfico de barras el número de centros
INAH por estado.
# Usando los datos de visitantes a los centros INAH en 2022
inah_df = pd.read_csv("inah_visitantes_2022.csv")
# Agrupando por estado y usando la función count()
inah_grouped = inah_df.groupby(by = "Estado").count()
inah_grouped = inah_grouped.reset_index() # Para que Estado no sea índice/label
# Mostrar grafico
sns.barplot(data = inah_grouped, x = "Tipo", y = "Estado")
Histograma vs gráfico de barras
Ambos gráficos parecen iguales, ambos usan barras, pero no son lo mismo.
Un histograma es un diagrama que muestra la frecuencia de datos numéricos,
mientras que el gráfico de barras compara tamaños de diferentes variables
categóricas.
Edición de gráficos
Modificar etiquetas de los ejes y exportar imagen como PNG.
# Declarar el grafico
ax = sns.barplot(data = inah_grouped, x = "Tipo", y = "Estado")
# Modificar las etiquetas de los ejes
ax.set_xlabel("Estado", fontsize = 12)
ax.set_ylabel("Número de Centros INAH", fontsize = 12)
# Ajustes para exportar imagen
plt.tight_layout()
plt.savefig('barplot_inah.png')
# Mostrar imagen
plt.show()
Girar ejes para mejorar la visualización.
# Misma boxplot de calificaciones de INECOL pero ahora los ejes invertidos
sns.boxplot(data = inecol_df, x = "resultado", y = "calificacion_final", whis = 1.5)
# Rotamos las etiquetas del eje x, 45 grados
plt.xticks(rotation=45)
plt.show()
Ejercicios
Usando los datos estudiantes_mxuk.csv, crear gráficos que muestren:
- Distribución de edad por universidad.
- Becas que tienen los estudiantes.
Usando los datos inah_visitantes_2022.csv:
- ¿Cuál es la visualización más representativa para mostrar el flujo de
visitantes en los meses reportados para un Centro INAH (o estado!)
determinado?
Referencias y material adicional
6. Análisis estadístico
Introducción
Python tiene bastantes librerías para realizar análisis estadístico. En esta
sección nos concentraremos en SciPy y statsmodels.
Datos
Usaremos los siguientes archivos para los ejercicios de este tema:
Librerías
Para esta sección usaremos las siguientes librerías:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
Datos de precipitación
Usaremos el archivo precipitacion_guerrero.csv que contiene datos históricos
mensuales y anuales de precipitación en Guerrero desde 1985 hasta 2020. La
descripción de las columnas es la siguiente:
| Variable | Tipo de variable | Descripción |
|---|
| PERIODO | Numérica | Año en el que se reporta información de precipitación |
| ENE | Numérica | Precipitación observada durante el mes de enero, en mm |
| FEB | Numérica | Precipitación observada durante el mes de febrero, en mm |
| MAR | Numérica | Precipitación observada durante el mes de marzo, en mm |
| ABR | Numérica | Precipitación observada durante el mes de abril, en mm |
| MAY | Numérica | Precipitación observada durante el mes de mayo, en mm |
| JUN | Numérica | Precipitación observada durante el mes de junio, en mm |
| JUN | Numérica | Precipitación observada durante el mes de junio, en mm |
| JUL | Numérica | Precipitación observada durante el mes de julio, en mm |
| AGO | Numérica | Precipitación observada durante el mes de agosto, en mm |
| SEP | Numérica | Precipitación observada durante el mes de septiembre, en mm |
| OCT | Numérica | Precipitación observada durante el mes de octubre, en mm |
| NOV | Numérica | Precipitación observada durante el mes de noviembre, en mm |
| DIC | Numérica | Precipitación observada durante el mes de diciembre, en mm |
| ANUAL | Numérica | Precipitación observada durante todo el periodo (año), en mm |
Puesto que estos datos usan comas para separar miles, el argumento thousands
indica a pandas el separador usado en estos datos. Ahora, importemos estos datos.
# Datos precipitacion
precipitacion = pd.read_csv("precipitacion_guerrero.csv", thousands = ",")
Inspeccionamos las medidas de estadística descriptiva.
# Estadistica descriptiva
precipitacion.describe()
Prueba de normalidad
Podemos observar normalidad utilizando histogramas como los que ofrece seaborn,
pero también podemos comprobar normalidad usando SciPy.
SciPy ofrece varias pruebas de normalidad, por ahora veremos la prueba
Shapiro-Wilk y D’Agostino-Pearson en sus funciones
stats.shapiro y
stats.normaltest
respectivamente.
Ambas pruebas se definen con las siguientes hipótesis:
Hipotesis nula:
$$H_{0}: \text{La muestra proviene de una distribución normal} $$
Hipotesis alternativa:
$$H_{1}: \text{La muestra no proviene de una distribución normal} $$
# Sintaxis de prueba de Shapiro-Wilk
stats.shapiro(muestra)
# Sintaxis de prueba D'Agostino-Pearson
stats.normaltest(muestra)
Para ambas pruebas, SciPy nos retornará el valor del estadístico y el valor-p
Hagamos una función para hacer prueba de normalidad con ambos métodos.
def normal_test(datos, option = "shapiro"):
if option != "shapiro":
test = stats.normaltest(datos)
else:
test = stats.shapiro(datos)
if test.pvalue < 0.05 :
print("Rechazar hipotesis nula")
else:
print("No hay evidencia suficiente para rechazar hipotesis nula")
print(test)
Ahora comprobemos si los datos de precipitación del mes de julio provienen de
una distribución normal.
# Prueba D'Agostino-Pearson
normal_test(precipitacion["JUL"], "dagostino")
Pruebas de hipótesis
Pruebas t
Una muestra
Esta prueba nos sirve para determinar si la media de la población estudiada es
igual a un valor conocido.
$$\mu = \mu_{0}$$
Definimos la hipótesis nula como:
$$H_{0}: \mu = \mu_{0} $$
Dependiendo el tipo de hipótesis alternativa, podemos tener las siguientes
opciones:
$$H_{0}: \mu \neq \mu_{0} \ \ \ (\text{dos colas}) $$
$$H_{0}: \mu < \mu_{0} \ \ o \ \ \mu > \mu_{0} \ \ \ (\text{una cola}) $$
Utilizaremos la función ttest_1samp
de SciPy.
# sintaxis
stats.ttest_1samp(a, popmean, alternative)
donde
a: Muestra
popmean: Valor de media conocido.
alternative: Parámetro opcional donde se define la hipótesis alternativa. Las
opciones disponibles son ’two-sided’ (dos colas), ’less’ y ‘greater’. El valor
predeterminado es ’two-sided’.
Hagamos una función para realizar la prueba de hipótesis.
def t_test_1samp(datos, media):
test = stats.ttest_1samp(datos, popmean = media)
if test.pvalue < 0.05:
print("Rechazar hipótesis nula")
else:
print("No hay evidencia suficiente para rechazar hipótesis nula")
print(test)
Probemos si la media de precipitación en julio es igual a 150.
t_test_1samp(precipitacion["JUL"], 150)
Dos muestras independientes
Esta prueba nos sirve para comparar las medias de dos muestras independientes
a y b, y determinar si son iguales.
$$\mu_{a} = \mu_{b}$$
Definimos la hipótesis nula como:
$$H_{0}: \mu_{a} = \mu_{b} $$
Dependiendo el tipo de hipótesis alternativa, podemos tener las siguientes
opciones:
$$H_{1}: \mu_{a} \neq \mu_{b} \ \ \ (\text{dos colas}) $$
$$H_{1}: \mu_{a} < \mu_{b} \ \ o \ \ \mu_{a} > \mu_{b} \ \ \ (\text{una cola}) $$
Utilizaremos la función ttest_ind de SciPy.
# sintaxis
stats.ttest_ind(a, b, equal_var, alternative)
donde
a y b: Muestras a contrastar
equal_var: Parámetro opcional que define si las muestras tienen varianzas
iguales.En caso de que sean iguales, SciPy hará la prueba de hipótesis usando la
prueba t-Student. Si las varianzas no son iguales, SciPy usará la prueba Welch.
El valor predeterminado es True.
alternative: Parámetro opcional donde se define la hipótesis alternativa. Las
opciones disponibles son ’two-sided’, ’less’ y ‘greater’. El valor
predeterminado es ’two-sided’.
SciPy nos retornará el estadístico y el valor-p.
Hagamos una pequeña función.
def t_test(muestra_a, muestra_b, equal_var):
t_test = stats.ttest_ind(a = muestra_a, b = muestra_b, equal_var= equal_var)
if t_test.pvalue < 0.05:
print("Rechazar hipótesis nula")
else:
print("No hay evidencia suficiente para rechazar hipótesis nula")
print(t_test)
Probemos contrastando las medias de precipitación de enero y marzo.
t_test(precipitacion["ENE"], precipitacion["MAR"], True)
Ahora probemos contrastando las medidas de precipitación de enero y julio. Es
importante recordar que la varianza entre ambos meses no es igual.
t_test(precipitacion["ENE"], precipitacion["JUL"], False)
Dos muestras dependientes (Prueba t pareada)
Esta prueba nos sirve para comparar las medias de dos muestras dependientes
a y b, y determinar si son iguales. Se considera que dos muestras son
dependientes o pareadas cuando existe una relación entre las observaciones. Por
ejemplo:
- Comprobar el nivel de satisfacción del mismo grupo de clientes, antes y después,
de cambiar detalles en el servicio.
- Comparar el progreso del mismo grupo de pacientes, antes y después, de
introducir un medicamento en su tratamiento.
En esta prueba se contrasta la diferencia entre las medias $\mu_d$. Si son
iguales, la diferencia será igual a 0.
Entonces, las hipótesis contrastadas son:
$$H_{0}: \mu_{d} = 0$$
$$H_{1}: \mu_{d} \neq 0$$
Es importante destacar que para que este tipo de pruebas sean relevantes, los
datos deben provenir de una distribución normal. Sin embargo, no es necesario
que las varianzas sean iguales.
SciPy tiene la función ttest_rel
para realizar este tipo de pruebas.
# sintaxis
stats.ttest_rel(a, b, alternative)
donde
a y b: Muestras a contrastar.
alternative: Parámetro opcional donde se define la hipótesis alternativa. Las
opciones disponibles son ’two-sided’, ’less’ y ‘greater’. El valor
predeterminado es ’two-sided’.
Escribimos una función para realizar esta prueba.
def t_test_dep(muestra_a, muestra_b):
t_test = stats.ttest_rel(a = muestra_a, b = muestra_b)
if t_test.pvalue < 0.05:
print("Rechazar hipotesis nula")
else:
print("No hay evidencia suficiente para rechazar hipotesis nula")
print(t_test)
Probemos esta función con los valores de medias de precipitación en julio.
Dividiremos la columna en dos series. Una serie para años anteriores a 2003, y
otra serie para años posteriores a 2003.
# Obtenemos los valores de precipitacion en julio, y los dividimos en dos partes
julio_85_02 = precipitacion.query('PERIODO <= 2002')["JUL"]
julio_03_20 = precipitacion.query('PERIODO >= 2003')["JUL"]
Ahora, probemos nuestra función.
# H0: La diferencia de medias es igual a 0
# H1: La diferencia de medias no es igual a 0
t_test_dep(julio_85_02, julio_03_20)
Prueba de Levene (Homogeneidad de varianzas)
La prueba de Levene es una prueba utilizada para evaluar la igualdad
(homogeneidad) de las varianzas para una variable calculada para dos o más
grupos. La prueba de Levene está definida como:
$$H_{0}: \sigma_{a} = \sigma_{b} = \sigma_{c} = … $$
$$H_{1}: \sigma_{a} \neq \sigma_{b} \neq \sigma_{c} \neq … \ \ \text{para al menos un par} $$
SciPy tiene implementada esta prueba en su función
stats.levene.
# Sintaxis
stats.levene(*muestras, center)
donde
muestras: las muestras a contrastar sus varianzas
center: este parámetro indica la medida de localización para centrar las
muestras. Los valores posibles son:
median - para muestras que provienen de distribuciones asimétricas. Este es
el valor predeterminado.
mean - para muestras que provienen de distribuciones simétricas
trimmed - para muestras que provienen de distribuciones con colas largas
(p. ej. distribución Cauchy)
SciPy nos retornará el estadístico y el valor-p.
Hagamos una pequeña función para verificar si las varianzas de la precipitación
promedio de los meses enero y marzo son iguales.
def levene_test(muestra_a, muestra_b, center):
levene_test = stats.levene(muestra_a, muestra_b, center= center)
if levene_test.pvalue < 0.05:
print("Rechazar hipotesis nula")
else:
print("No hay evidencia suficiente para rechazar hipotesis nula")
print(levene_test)
Como prueba de cordura, veamos las distribuciones de la precipitación en ambos
meses usando histogramas.
sns.histplot(precipitacion["ENE"])
sns.histplot(precipitacion["MAR"])
Ahora hagamos la prueba de Levene.
levene_test(precipitacion["ENE"], precipitacion["MAR"], "median")
Regresión lineal
La regresión lineal es un instrumento matemático usado para modelar las
relaciones entre una variable dependiente (o variable de respuesta), y una o más
variables independientes (o variables explicatorias). El modelo lineal tiene la
siguiente forma,
$$y = \beta_{0} + \beta_{i}x_i + … + \epsilon_i \ \ \ \ \ i = 1, … n $$
donde,
$\beta_i$ representan los coeficientes que describen la relación o la influencia
que tiene la variable $x_i$ sobre la variable dependiente.
$\beta_0$ representa el intercepto. Este valor describe la relación entre la
variable dependiente y las variables independientes $x_i$, cuando $x_i$ = 0.
$x_i$ son las variables independientes utilizadas en el modelo.
$\epsilon_i$ representa el error aleatorio que se introduce en el modelo por cada
variable independiente $x_i$. Estos errores son independientes y siguen una
distribución normal. $\epsilon_i \sim \mathcal{N}(0, \sigma^2) $
Mínimos cuadrados ordinarios
Existen distintos métodos para determinar los coeficientes $\beta$, uno de ellos es
mínimos cuadrados ordinarios. statsmodels es una librería de Python que
contiene una colección grande de modelos estadísticos. Para ajustar un modelo
lineal usando mínimos cuadrados ordinarios, usaremos la función
ols
(ordinary least squares, en inglés).
from statsmodels.formula.api import ols
Ahora usaremos los datos edadpesograsas.txt que nos servirá para entender el
uso de ols. Este archivo contiene información de edad, peso y cantidad de
grasas en 25 pacientes. La descripción de las columnas es la siguiente:
| Variable | Tipo de variable | Descripción |
|---|
| peso | Numérica | Peso corporal, en kg |
| edad | Numérica | Edad |
| grasas | Numérica | Colesterol, en mg/dl |
Lo primero que haremos es importar los datos. Como estos datos provienen de un
archivo de texto (*.txt), usaremos ahora el método
read_table()
de pandas. El separador usado en este archivo es un tabulador. Daremos esta
información al método para que el archivo se importe correctamente usando el
argumento sep.
# Importar datos
edad_peso = pd.read_table("edadpesograsas.txt", sep="\t")
La sintaxis de ols es la siguiente:
model = ols('variable_dependiente ~ variable1 + variable2 + ... +', df).fit()
Intentemos modelar la cantidad de grasas respecto a la edad:
model = ols('grasas ~ edad', edad_peso).fit()
Para revisar la información del modelo de regresion, usamos el método summary()
# Ver resultados
model.summary()
Ahora agreguemos la variable peso al modelo de regresión:
model = ols('grasas ~ edad + peso', edad_peso).fit()
¿Mejoró el modelo?
Regresión paso a paso
Lo que acabamos de hacer se llama regresión paso a paso (stepwise regression,
en inglés). Esta metodología es iterativa, pues implica seleccionar variables
de forma automática y ver como mejora (o empeora) el modelo. Existen dos tipos
de selección:
Selección hacia adelante (Forward selection, en inglés): En este tipo de
selección, el modelo se inicia sin ninguna variable. Después se agrega una
variable a la vez y se prueba si mejoró la calidad del modelo con la inclusión
de dicha variable.
Selección hacia atrás (Backward selection, en inglés) En este tipo de
selección, se inicia con un modelo que incluye todas las variables. Después se
elimina una variable a la vez y se prueba si mejoró la calidad del modelo con la
eliminación de dicha variable.
Este método es adecuado cuando se tiene una cantidad significativa de variables
que explican el fenómeno a modelar y se desea empezar a eliminar variables
irrelevantes. Sin embargo, siempre se preferirá analizar y entender los datos
antes de crear modelos.
Con esto concluimos este tema.
Referencias y material adicional
7. Recapitulación
Introducción
Ahora que hemos aprendido sobre como usar las librerías de manipulación de datos,
visualizaciones y análisis estadístico, hagamos un pequeño ejercicio.
Datos
Usaremos el siguiente archivo para recapitular todo lo aprendido:
Estos son datos recopilados por INEGI en su encuesta ENDUTIH de 2019. La
descripción de las columnas es la siguiente:
| Variable | Tipo variable | Descripción pregunta |
|---|
| energia_electrica | Binaria | La vivienda dispone de energía eléctrica |
| refrigerador | Binaria | La vivienda dispone de refrigerador |
| lavadora | Binaria | La vivienda dispone de lavadora |
| auto_propio | Binaria | Las personas viviendo en esta vivienda disponen de automóvil o camioneta |
| personas_vivienda | Numérica | Número de personas viviendo normalmente en la vivienda |
| mismo_gasto | Binaria | El gasto para comer de todas las personas viviendo en la vivienda es el mismo |
| TLOC | Numérica (ordinal) | Tamaño de la Localidad (1: 100 000 y más habitantes, 2: 15 000 a 99 999 habitantes, 3: 2 500 a 14 999 habitantes, 4: menor a 2500 habitantes) |
| ESTRATO | Numérica (ordinal) | Estrato socioeconómico. (1: Bajo, 2: Medio bajo, 3: Medio alto, 4: Alto) |
| material_1 | Binaria | El material predominante del piso de esta vivienda es tierra |
| material_2 | Binaria | El material predominante del piso de esta vivienda es cemento |
| material_3 | Binaria | El material predominante del piso de esta vivienda es madera, mosaico u otro |
| fuente_agua_1 | Binaria | La fuente de agua es agua entubada dentro de la vivienda |
| fuente_agua_2 | Binaria | La fuente de agua es agua entubada fuera de la vivienda, pero dentro del terreno |
| fuente_agua_3 | Binaria | La fuente de agua es agua entubada de llave pública (o hidrante) |
| fuente_agua_4 | Binaria | La fuente de agua es agua entubada que acarrean de otra vivienda |
| fuente_agua_5 | Binaria | La fuente de agua es agua de pipa |
| fuente_agua_6 | Binaria | La fuente de agua de la vivienda es agua de un pozo, río, arroyo, lago u otro |
| conexion_drenaje_1 | Binaria | La vivienda tiene drenaje o desagüe conectado a la red pública |
| conexion_drenaje_2 | Binaria | La vivienda tiene drenaje o desagüe conectado a una fosa séptica |
| conexion_drenaje_3 | Binaria | La vivienda tiene drenaje o desagüe conectado a una tubería que va a dar a una barranca o grieta |
| conexion_drenaje_4 | Binaria | La vivienda tiene drenaje o desagüe conectado a una tubería que va a dar a un río, lago o mar |
| conexion_drenaje_5 | Binaria | La vivienda no tiene drenaje o desagüe |
| tipo_poblacion_R | Binaria | La vivienda se encuentra en una población rural |
| tipo_poblacion_U | Binaria | La vivienda se encuentra en una población urbana |
Inspección de datos
Empezamos importando las librerías que usaremos y los datos.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from statsmodels.formula.api import ols
Ahora importemos los datos y revisemos el tamaño del DataFrame.
encuesta_vivienda = pd.read_csv("endutih_vivienda_anual_2019_enc.csv")
encuesta_vivienda.shape
Esto nos devuelve la tupla (21163, 24). Es un set de datos grande. Pero no es
problema para Python.
Análisis exploratorio
Ahora veamos las medidas de estadistíca descriptiva.
encuesta_vivienda.describe()
Tal vez estos resultados no nos ayuden mucho puesto que son datos con mayormente
variables binarias (0 y 1).
Matriz de correlaciones
La matriz de correlaciones se puede obtener con pandas usando el método
corr().
Las correlaciones pueden calcularse usando distintos métodos como Pearson,
Spearman y Kendall usando el argumento method.
Para este caso, utilizaremos Spearman como método puesto que la mayor parte de
las variables son binarias y sólo dos son de tipo ordinal.
corr_matrix = encuesta_vivienda.corr(method = "spearman")
Esto nos devuelve otro DataFrame con la matriz de correlaciones. Este nuevo
DataFrame tiene un tamaño de 24 x 24.
Visualizaciones
Podemos ver la matriz de correlaciones con una visualización llamada
heatmap.
# Heatmap
plt.figure(figsize = (18,12)) # Hacer más grande la figura
sns.heatmap(corr_matrix, annot = True, cmap = "Blues")
Hemos pasado un par de argumentos nuevos. annot nos reportará el valor del
factor de correlación en la visualización. cmap es el mapa de colores que
que seaborn usará. Para mejorar la vista, hemos usado la paleta Blues. Si el
factor de correlación se acerca más al valor 1, el cuadro tendrá un color azul
más fuerte. Si te interesa ver más opciones puedes ver la documentación de
colormaps de
matplotlib.
Adicionalmente, por ser una visualización de 24x24, el tamaño de la figura debe
ser más grande.
Enfoquémonos en las variables ESTRATO y TLOC, que son numéricas.
sns.histplot(encuesta_vivienda["ESTRATO"])
Podemos ver que es una variable discreta, puesto que tiene valores enteros que
van del 1 al 5. Podemos ver que hay menos personas con un estrato 4 (estrato
alto), mientras que la mayor parte de las respuestas tienen un estrato 2
(estrato medio bajo).
sns.histplot(encuesta_vivienda["TLOC"])
De igual manera, TLOC es una variable discreta. Los grupos de encuestados más
representativos en la muestra, son de localidades con 100,000 y más habitantes,
y de localidades con menos de 2500 habitantes.
Tracemos una recta entre ambas variables para encontrar más relaciones.
sns.lineplot(data = encuesta_vivienda, x = "TLOC", y = "ESTRATO")
Podemos ver que conforme aumenta TLOC, ESTRATO decrece. Parece tener sentido.
Modelo de regresión lineal
Nos interesa entender cuáles son las variables que definen el estrato
socioeconómico de una familia.
Podríamos empezar haciendo un modelo usando regresión paso a paso. O también,
usando las variables que tienen más correlación con el estrato socioeconómico.
# Ajuste de datos
formula = "ESTRATO ~ material_3 + fuente_agua_1 + TLOC + tipo_poblacion_U + \
conexion_drenaje_1 + refrigerador + lavadora + auto_propio"
modelo_ols = ols(formula, encuesta_vivienda).fit()
Trivia
¿Por qué no agregar tipo_poblacion_R también?
Con este modelo, estamos teorizando que el estrato depende de dichas variables.
Inspeccionemos el modelo.
# Revisar modelo
modelo_ols.summary()
Obtuvimos un modelo con un $R^2$ ajustado de 0.527. Adicionalmente, statsmodels
nos devuelve los parámetros $\beta_i$ con su respectivo intervalo de confianza,
y una prueba t sobre cada parámetro.
Prueba t en coeficientes de regresión
La prueba t contrasta si el parámetro $\beta_i$ calculado es relevante para
ajustar los datos o no. Las hipótesis están definidas como:
$$H_0: \beta_i = 0 $$
$$H_1: \beta_i \neq 0 $$
Asimismo, nos regresa los valores-p de dicha prueba. (¿Cuándo rechazábamos la
hipótesis nula?)
Evaluación del modelo
Veamos qué tal predice nuestro modelo el estrato socioeconómico.
Para acceder a las predicciones de nuestro modelo, llamamos al método predict()
del modelo de regresión.
# Predicción del modelo
Y_pred = modelo_ols.predict()
Esta prediccion es un arreglo de NumPy, que es un tipo de datos optimizado
para contener matrices.
Para evaluar nuestro modelo, tenemos que contrastar los valores observados de
la variable dependiente con los valores predecidos por el modelo. Para esto,
podemos crear un nuevo DataFrame conteniendo esta informacion como columnas.
He creado la siguiente función que se encargará de todo.
# Una funcion para evaluar nuestro modelo
def model_evaluation(y_obs, y_pred):
'''
Esta función calculara las métricas RMSE y MAE de un modelo de regresión
lineal.
inputs:
y_obs: una serie de pandas que contiene los valores observados
de la variable dependiente
y_pred: un arreglo que contiene los valores predecidos
de la variable dependiente utilizando el modelo de regresion de
statsmodels
output:
model_eval: un dataframe de pandas que contiene los errores de
regresion, asi como los valores observados y predecidos de la
variable dependiente.
'''
# Convertir variable predecida a una serie
y_pred = pd.Series(y_pred)
# Concatenar valores en un solo dataframe
model_eval = pd.concat([y_obs, y_pred], keys = ["y_obs", "y_pred"], axis = 1)
# Calcular errores
model_eval["error"] = model_eval["y_obs"] - model_eval["y_pred"]
model_eval["sq_error"] = (model_eval["error"])**2
model_eval["abs_error"] = abs(model_eval["error"])
# Calculo de MAE y RMSE
MAE = model_eval["abs_error"].sum()/model_eval["abs_error"].count()
RMSE = (model_eval["sq_error"].sum()/model_eval["sq_error"].count())**(1/2)
print("Métricas")
print("MAE: {} \t RMSE: {}".format(MAE, RMSE))
return model_eval
En esta función estamos concatenando (“juntando”) las series usando
concat().
Después se calcularon 3 columnas de error. El error se define como la diferencia
del valor observado $y_i$ menos valor predecido $\hat{y}_i$.
- Error: $y_i - \hat{y}_i$
- Error cuadrado: $(y_i - \hat{y}_i)^2$
- Error absoluto: $| y_i - \hat{y}_i |$
Estos errores nos sirven para definir las siguientes métricas:
$$\text{MAE} = \frac{\sum_{i=1}^{N}| y_i - \hat{y}_i |}{N} \ \ \ \ \ \ \ \text{(Error absoluto medio)}$$
$$\text{RMSE} = \sqrt{\frac{\sum_{i=1}^{N}( y_i - \hat{y}_i )^2}{N}} \ \ \ \ \ \ \ \text{(Raíz del error cuadrático medio)}$$
Estas métricas son utilizadas para determinar la calidad del modelo de regresión
implementado.
Ahora usemos la función con nuestros datos.
comparison = model_evaluation(encuesta_vivienda["ESTRATO"], modelo_ols.predict())
comparison
Esto nos devuelve el DataFrame con los valores observados, predecidos, errores e
imprime las métricas del modelo.
Métricas
MAE: 0.5490078148166975 RMSE: 0.7043990103948065
Trivia
¿Qué nos dice cada métrica?
Conclusión
Si bien la variable dependiente es una variable numérica, es una variable ordinal.
Una regresión lineal asume que la variable dependiente es una variable númerica
continua. Este ejercicio fue diseñado para demostrar como utilizar Python para
analizar datos, encontrar tendencias usando visualizaciones, e implementar un
modelo de regresión basándonos en estas tendencias.
Lo más correcto para estos datos sería implementar un modelo de regresión
ordinal. Pero esos son otros temas de modelos de regresión generalizados…
# Aqui van tus comentarios ;)
Referencias y material adicional
Extras
Introducción
En esta sección se presentan temas adicionales que pueden ser de interés para
grupos específicos.
Instalación de paquetes
Anaconda es una distribución que trae muchos paquetes y librerías de Python
precargados, facilitando el uso del lenguaje para varias tareas. Sin embargo, a
veces es necesario instalar otros paquetes que Anaconda no trae.
La instalación de paquetes se realiza en una sesión de Terminal (macOS / Linux)
o Anaconda Prompt (Windows) con el siguiente comando.
pip install <nombre-paquete>
pip es el gestor de paquetes predeterminado de Python y se encargará de traer
los archivos necesarios (y dependencias) de los paquetes que instalemos.
También existe conda, que es el gestor predeterminado de Anaconda.
A veces conda es más eficiente para ciertos paquetes…
conda install -<opciones> conda-forge <nombre-paquete>
Alfa de Cronbach
Esta medida la podemos calcular rápidamente usando el paquete
pingouin. pingouin es una librería
mucho más nueva que statsmodels y Scipy, que busca hacer más accesibles cálculos
estadísticos. Pingouin puede procesar DataFrames de pandas nativamente.
Instalación
En una sesión de Terminal (macOS / Linux) o Anaconda Prompt
(Windows), lancemos el siguiente comando:
o también
conda install -c conda-forge pingouin
La instalación es rápida y termina en menos de 5 minutos.
Uso
El siguiente ejemplo contiene los resultados de una encuesta ficticia de 3
preguntas con escala Likert de 3 puntos.
import pandas as pd
import pingouin as pg
# Respuestas de una encuesta
encuesta = pd.DataFrame({'Q1': [1, 2, 2, 3, 2, 2, 3, 3, 2, 3],
'Q2': [1, 1, 1, 2, 3, 3, 2, 3, 3, 3],
'Q3': [1, 1, 2, 1, 2, 3, 3, 3, 2, 3]})
Para calcular el alfa de Cronbach, usamos la función
cronbach_alpha()
de pingouin.
# Calculo de alfa de Cronbach
pg.cronbach_alpha(data = encuesta)
Esto nos devolverá una tupla que contiene el valor calculado del alfa de
Cronbach, y su intervalo de confianza al 95%.
(0.7734375, array([0.336, 0.939]))
Si uno desea cambiar el intervalo de confianza, se puede hacer con el argumento
ci. El intervalo de confianza se expresa como fracción.
# Alfa de Cronbach e intervalo de confianza al 99%
pg.cronbach_alpha(data = encuesta, ci = 0.99)
Referencias y material adicional

